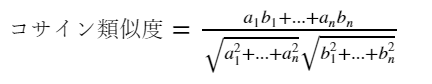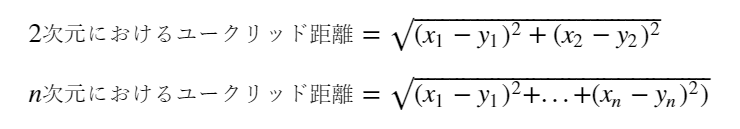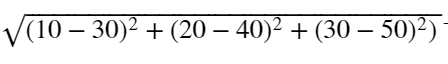クラスタリングの性能評価関数にSSE(クラスタ内誤差平方和)がある
SSEにより様々なk-meansクラスタリングの性能を評価可能。
SSEの式
print(‘Distortion: %.2f’% km.inertia_)
クラスタ内誤差平方和を出力、クラスターの数を調整して一番低いものが正確
|
1 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
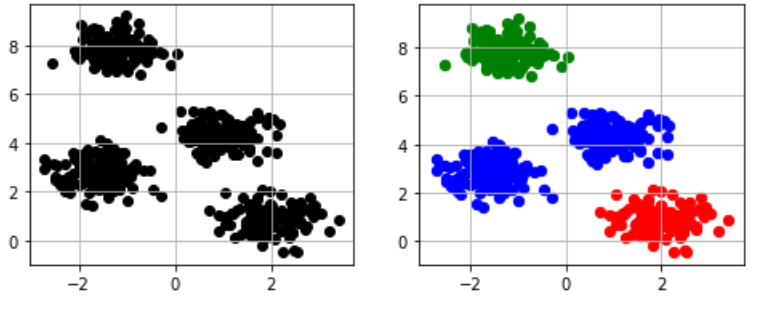
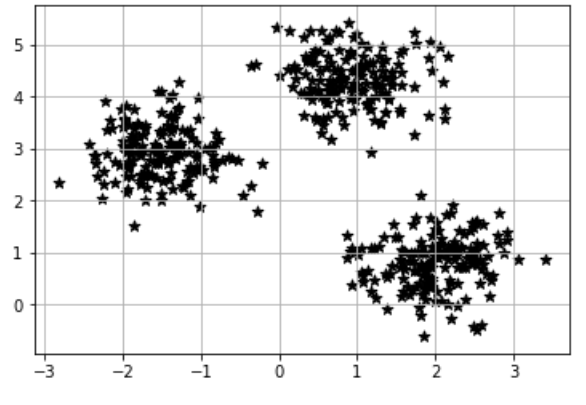
import matplotlib.pyplot as plt import numpy as np import pandas as pd from sklearn.cluster import KMeans from sklearn.datasets import make_blobs # Xには1つのプロットの(x,y)が、yにはそのプロットの所属するクラスター番号が入る X,y = make_blobs(n_samples=150, # サンプル点の総数 n_features=2, # 特徴量(次元数)の指定 default:2 centers=3, # クラスタの個数 cluster_std=0.5, # クラスタ内の標準偏差 shuffle=True, # サンプルをシャッフル random_state=0) # 乱数生成器の状態を指定 km = KMeans(n_clusters=3, # クラスターの個数 init='k-means++', # セントロイドの初期値をランダムに設定 default: 'k-means++' n_init=10, # 異なるセントロイドの初期値を用いたk-meansの実行回数 max_iter=300, # k-meansアルゴリズムを繰り返す最大回数 tol=1e-04, # 収束と判定するための相対的な許容誤差 random_state=0) # 乱数発生初期化 y_km = km.fit_predict(X) # クラスターが存在するデータを渡し、各サンプルに対するクラスタ番号を求める plt.scatter(X[y_km==0,0], # y_km(クラスター番号)が0の時にXの0列目を抽出 X[y_km==0,1], # y_km(クラスター番号)が0の時にXの1列目を抽出 s=50, c='r', marker='*', label='cluster 1') plt.scatter(X[y_km==1,0], X[y_km==1,1], s=50, c='b', marker='*', label='cluster 2') plt.scatter(X[y_km==2,0], X[y_km==2,1], s=50, c='g', marker='*', label='cluster 3') plt.scatter(km.cluster_centers_[:,0], # km.cluster_centers_には各クラスターのセントロイドの座標が入っている km.cluster_centers_[:,1], s=250, marker='*', c='black', label='centroids') plt.legend(loc="best") plt.grid() plt.show() print('Distortion: %.2f'% km.inertia_) #クラスタ内誤差平方和を出力、クラスターの数を調整して一番低いものが正確 |
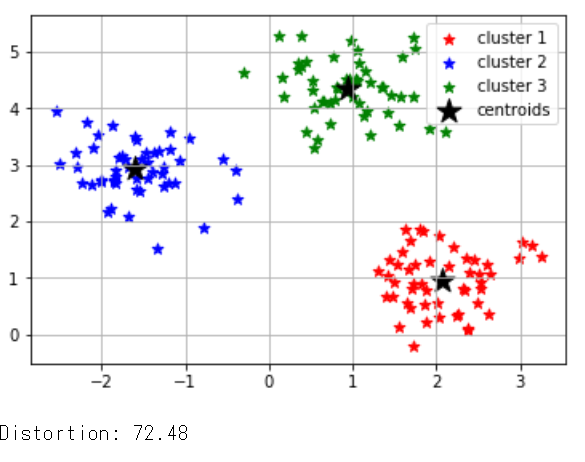
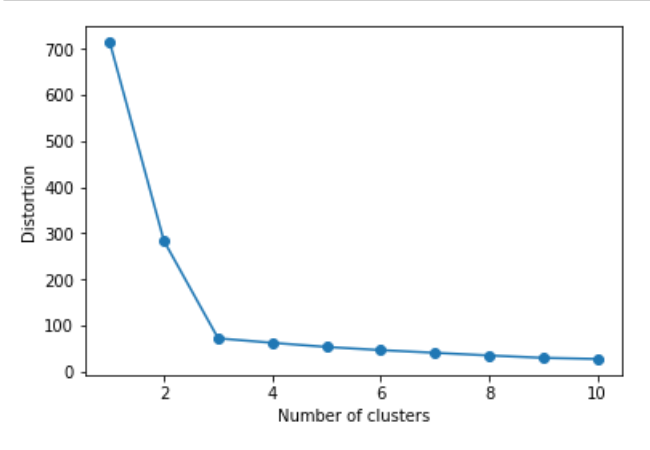
しかし、この方法だと一度に一つのクラスタだけしか評価できないのでエルボー法により
forを10回回して10個分のSSEをグラフに表示させ、急降下している部分を見つける事が可能
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import matplotlib.pyplot as plt import numpy as np import pandas as pd from sklearn.cluster import KMeans from sklearn.datasets import make_blobs # Xには1つのプロットの(x,y)が、yにはそのプロットの所属するクラスター番号が入る X,y = make_blobs(n_samples=150, # サンプル点の総数 n_features=2, # 特徴量(次元数)の指定 default:2 centers=3, # クラスタの個数 cluster_std=0.5, # クラスタ内の標準偏差 shuffle=True, # サンプルをシャッフル random_state=0) # 乱数生成器の状態を指定 km = KMeans(n_clusters=3, # クラスターの個数 init='k-means++', # セントロイドの初期値をランダムに設定 default: 'k-means++' n_init=10, # 異なるセントロイドの初期値を用いたk-meansの実行回数 max_iter=300, # k-meansアルゴリズムを繰り返す最大回数 tol=1e-04, # 収束と判定するための相対的な許容誤差 random_state=0) # 乱数発生初期化 y_km = km.fit_predict(X) # クラスターが存在するデータを渡し、各サンプルに対するクラスタ番号を求める distortions = [] for i in range(1,11): # 1~10クラスタまで一気に計算 km = KMeans(n_clusters=i, init='k-means++', # k-means++法によりクラスタ中心を選択 n_init=10, max_iter=300, random_state=0) km.fit(X) # クラスタリングの計算を実行 distortions.append(km.inertia_) # km.fitするとkm.inertia_が得られる plt.plot(range(1,11),distortions,marker='o') plt.xlabel('Number of clusters') plt.ylabel('Distortion') plt.show() |