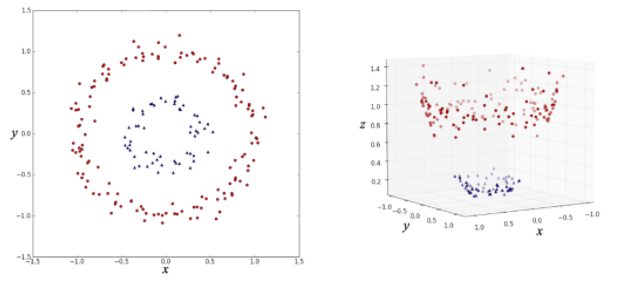
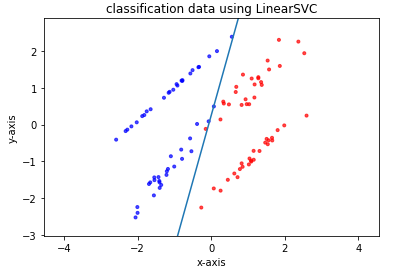
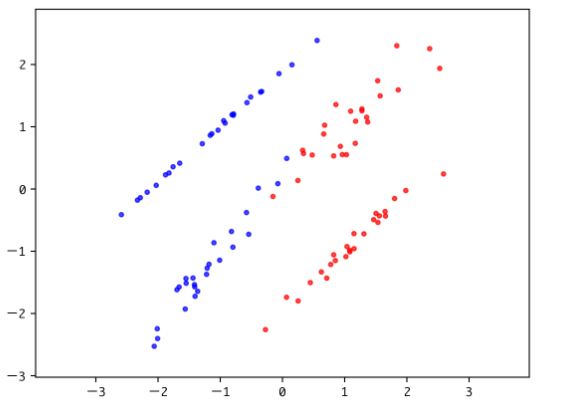
決定木はこれまで紹介したロジスティック回帰やSVMとは違い、データの要素(説明変数)の一つ一つに着目し、その要素内でのある値を境にデータを分割していくことでデータの属するクラスを決定しようとする手法です。
決定木では説明変数の一つ一つが目的変数にどのくらいの影響を与えているのかを見ることができます。
分割を繰り返すことで枝分かれしていきますが、先に分割される変数ほど影響力が大きいと捉えることができます。
欠点は線形分離可能なデータは苦手であることと、学習が教師データに寄りすぎる(汎化されない)ことです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
# きのこデータの取得 # 必要なパッケージをインポート import requests import zipfile from io import StringIO import io import pandas as pd # データの前処理に必要なパッケージのインポート from sklearn.model_selection import train_test_split from sklearn import preprocessing # url mush_data_url = "http://archive.ics.uci.edu/ml/machine-learning-databases/mushroom/agaricus-lepiota.data" s = requests.get(mush_data_url).content # データの形式変換 mush_data = pd.read_csv(io.StringIO(s.decode('utf-8')), header=None) # データに名前をつける(データを扱いやすくするため) mush_data.columns = ["classes", "cap_shape", "cap_surface", "cap_color", "odor", "bruises", "gill_attachment", "gill_spacing", "gill_size", "gill_color", "stalk_shape", "stalk_root", "stalk_surface_above_ring", "stalk_surface_below_ring", "stalk_color_above_ring", "stalk_color_below_ring", "veil_type", "veil_color", "ring_number", "ring_type", "spore_print_color", "population", "habitat"] # カテゴリー変数(色の種類など数字の大小が決められないもの)をダミー特徴量(yes or no)として変換する mush_data_dummy = pd.get_dummies( mush_data[['gill_color', 'gill_attachment', 'odor', 'cap_color']]) # 目的変数:flg立てをする mush_data_dummy["flg"] = mush_data["classes"].map( lambda x: 1 if x == 'p' else 0) # 説明変数と目的変数 X = mush_data_dummy.drop("flg", axis=1) Y = mush_data_dummy['flg'] # 学習データとテストデータに分ける train_X, test_X, train_y, test_y = train_test_split(X,Y, random_state=42) # 以下にコードを記述してください。 # モデルの読み込み from sklearn.tree import DecisionTreeClassifier # モデルの構築 model = DecisionTreeClassifier() # モデルの学習 model.fit(train_X, train_y) # 正解率を算出 print(model.score(test_X, test_y)) |