|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
様々な分類の手法について実際にコードを動かして学ぶ際に、分類ができそうなデータを用意する必要があります。 実用レベルでは実際に測定された何かしらの値を入手するところから始めますが、今回はその部分は省き、架空の分類用データを自分で作成してしまいましょう。 分類に適したデータを作成するには、scikit-learn.datasetsモジュールのmake_classification() 関数を使います。 make_classificationの引数 # モジュールのimport from sklearn.datasets import make_classification # データX, ラベルyの生成 X, y = make_classification(n_samples, n_classes, n_features, n_redundant, random_state) 上記関数の各引数は以下のとおりです n_samples 用意するデータの個数 n_classes クラス数。デフォルトは2 n_features データの特徴量の個数 n_redundant 分類に不要な特徴量(余分な特徴量)の個数 random_state 乱数のシード(乱数のパターンを決定する要素) 他にも引数はありますが、この章ではこれらを定義したデータを作成していきます。 また、データがどのクラスに属しているかを示す「ラベル(y)」が用意されますが、基本的に整数値によってラベルを用意します。 例えば二項分類であれば各データのラベルは「0」または「1」になります。 |
- n_classes
クラス数。デフォルトは2 - n_features
データの特徴量の個数 - n_redundant
分類に不要な特徴量(余分な特徴量)の個数 - random_state
乱数のシード(乱数のパターンを決定する要素)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
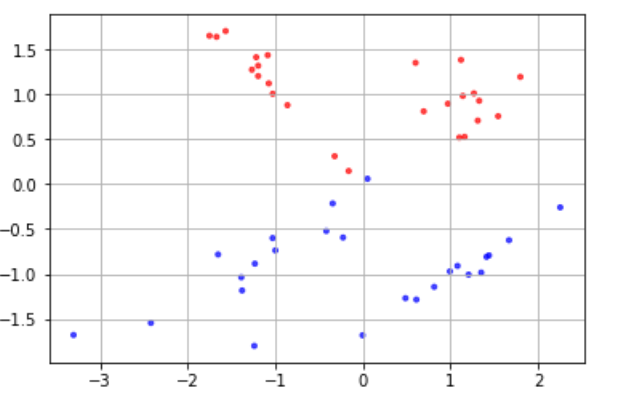
# モジュールのimport from sklearn.datasets import make_classification # プロット用モジュール import matplotlib.pyplot as plt import matplotlib %matplotlib inline # コード # データX, ラベルyを生成 X, y = make_classification(n_samples=50, n_features=2, n_redundant=0, random_state=0) # データの色付け、プロット plt.scatter(X[:, 0], X[:, 1], c=y, marker='.', cmap=matplotlib.cm.get_cmap(name='bwr'), alpha=0.7) plt.grid(True) |
|
1 2 3 |
他にも引数はありますが、この章ではこれらを定義したデータを作成していきます。 また、データがどのクラスに属しているかを示す「ラベル(y)」が用意されますが、基本的に整数値によってラベルを用意します。 例えば二項分類であれば各データのラベルは「0」または「1」になります。 |