プログラミング

ロジスティック回帰

2017年12月13日 by 河副太智 Leave a Comment

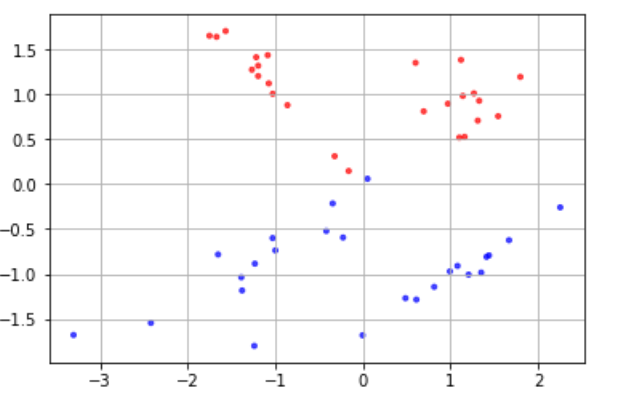
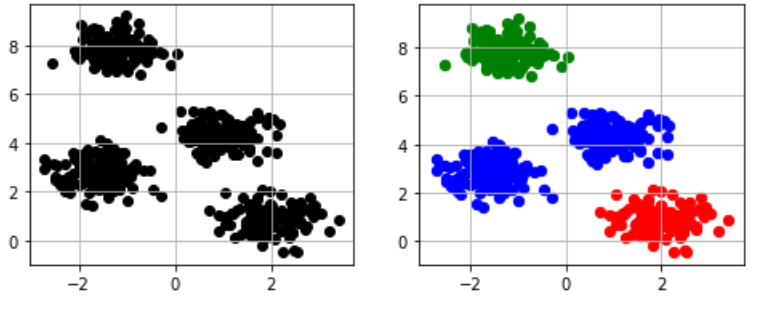
ロジスティック回帰は線形分離可能なデータの境界線を学習によって見つけてデータの分類を行なう手法です。

特徴としては境界線が直線になることです。
また、データがクラスに分類される確率も計算することが可能です。

欠点としては教師データが線形分離可能でないと分類ができないということです。
また、教師データから学習した境界線はクラスの端にあるデータのすぐそばを通るようになるため、一般化した境界線になりにくい（汎化能力が低い）ことも欠点です。

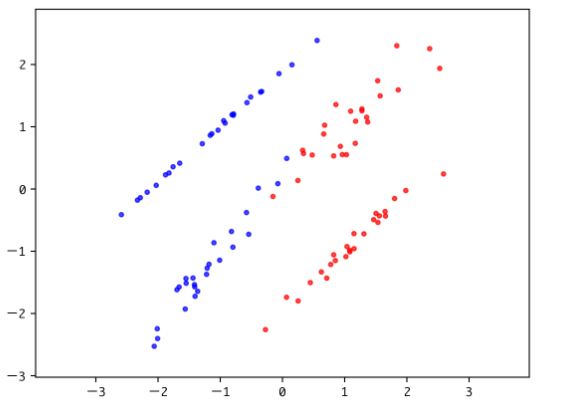
実装
ロジスティック回帰モデルはscikit-learnライブラリのlinear_modelサブモジュール内にLogisticRegression()として定義されています。
ロジスティック回帰モデルを使って学習する場合、次のようなコードを書いてモデルを呼び出します。
# パッケージからモデルを呼び出す
from sklearn.linear_model import LogisticRegression

# モデルを構築する
model = LogisticRegression()

# モデルに学習させる
# train_data_detailはデータのカテゴリーを予測するために使う情報をまとめたもの
# train_data_labelはデータの属するクラスのラベル
model.fit(train_data_detail, train_data_label)

# モデルに予測させる
model.predict(data_detail)

# モデルの予測結果の正解率
model.score(data_detail, data_true_label)
今回は座標によって属するクラスを識別しているため、グラフでモデルがどのような境界線を学習したのか見ることができます。
境界線は直線なので、y = ax+b の形で表現されます、以下のXi, Yはその直線を求めている過程になります。
グラフの視覚化にはmatplotlibライブラリを使います。
# パッケージをインポート
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# ページ上で直接グラフが見られるようにするおまじない
%matplotlib inline

# 生成したデータをプロット
plt.scatter(X[:, 0], X[:, 1], c=y, marker=’.’,
cmap=matplotlib.cm.get_cmap(name=’bwr’), alpha=0.7)

# 学習して導出した識別境界線をプロット
# model.coef_はデータの各要素の重み（傾き）を、
# model.intercept_はデータの要素全部に対する補正（切片）を表す。
Xi = np.linspace(-10, 10)
Y = -model.coef_[0][0] / model.coef_[0][1] * \
Xi – model.intercept_ / model.coef_[0][1]
plt.plot(Xi, Y)

# グラフのスケールを調整
plt.xlim(min(X[:, 0]) – 0.5, max(X[:, 0]) + 0.5)
plt.ylim(min(X[:, 1]) – 0.5, max(X[:, 1]) + 0.5)
plt.axes().set_aspect(‘equal’, ‘datalim’)
# グラフにタイトルを設定する
plt.title(“classification data using LogisticRegression”)
# x軸、y軸それぞれに名前を設定する
plt.xlabel(“x-axis”)
plt.ylabel(“y-axis”)
plt.show()

# パッケージをインポート
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
# ページ上で直接グラフが見られるようにするおまじない
%matplotlib inline

# データの生成
X, y = make_classification(n_samples=100, n_features=2,
                           n_redundant=0, random_state=42)
train_X, test_X, train_y, test_y = train_test_split(X, y, random_state=42)

# 以下にコードを記述してください
# モデルの構築
model = LogisticRegression(random_state=42)

# train_Xとtrain_yを使ってモデルに学習させる
model.fit(train_X, train_y)

# test_Xに対するモデルの分類予測結果
pred_y = model.predict(test_X)

# 生成したデータをプロット
plt.scatter(X[:, 0], X[:, 1], c=y, marker='.',
            cmap=matplotlib.cm.get_cmap(name='bwr'), alpha=0.7)

# 学習して導出した識別境界線をプロット
Xi = np.linspace(-10, 10)
Y = -model.coef_[0][0] / model.coef_[0][1] * \
    Xi - model.intercept_ / model.coef_[0][1]
plt.plot(Xi, Y)

# グラフのスケールを調整
plt.xlim(min(X[:, 0]) - 0.5, max(X[:, 0]) + 0.5)
plt.ylim(min(X[:, 1]) - 0.5, max(X[:, 1]) + 0.5)
plt.axes().set_aspect('equal', 'datalim')
# グラフにタイトルを設定する
plt.title("classification data using LogisticRegression")
# x軸、y軸それぞれに名前を設定する
plt.xlabel("x-axis")
plt.ylabel("y-axis")
plt.show()

# パッケージをインポート

import numpy as np

import matplotlib

import matplotlib.pyplot as plt

from sklearn.linear_model import LogisticRegression

from sklearn.model_selection import train_test_split

from sklearn.datasets import make_classification

# ページ上で直接グラフが見られるようにするおまじない

%matplotlib inline

# データの生成

X, y = make_classification(n_samples=100, n_features=2,

n_redundant=0, random_state=42)

train_X, test_X, train_y, test_y = train_test_split(X, y, random_state=42)

# 以下にコードを記述してください

# モデルの構築

model = LogisticRegression(random_state=42)

# train_Xとtrain_yを使ってモデルに学習させる

model.fit(train_X, train_y)

# test_Xに対するモデルの分類予測結果

pred_y = model.predict(test_X)

# 生成したデータをプロット

plt.scatter(X[:, 0], X[:, 1], c=y, marker='.',

cmap=matplotlib.cm.get_cmap(name='bwr'), alpha=0.7)

# 学習して導出した識別境界線をプロット

Xi = np.linspace(-10, 10)

Y = -model.coef_[0][0] / model.coef_[0][1] * \

Xi - model.intercept_ / model.coef_[0][1]

plt.plot(Xi, Y)

# グラフのスケールを調整

plt.xlim(min(X[:, 0]) - 0.5, max(X[:, 0]) + 0.5)

plt.ylim(min(X[:, 1]) - 0.5, max(X[:, 1]) + 0.5)

plt.axes().set_aspect('equal', 'datalim')

# グラフにタイトルを設定する

plt.title("classification data using LogisticRegression")

# x軸、y軸それぞれに名前を設定する

plt.xlabel("x-axis")

plt.ylabel("y-axis")

plt.show()

scikit-learnで学習と予測

2017年12月13日 by 河副太智 Leave a Comment

機械学習において、学習方法は複数存在します。
学習方法のことをモデルと呼ぶことにします。
(厳密には学習方法ではなく教師データから学習を行い、ラベルを予測するまでの一連の流れの概形のことを指します。)

また、機械学習によってデータの分類ができるプログラムのことを分類器と呼ぶことにしましょう。

機械学習のモデルを全て自分で実装するのは大変ですが、
Pythonには機械学習に特化したライブラリがたくさん存在します。
その中でもscikit-learnは機械学習のモデルがあらかじめ用意されたライブラリです。

架空のモデルClassifierを例にした使い方は下のコードを見てください。
# モジュールのインポート
# モデルごとに別のモジュールを参照する
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC, SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier

# モデルの構築
model = Classifier()
# モデルの学習
model.fit(train_X, train_y)
# モデルによるデータの予測
model.predict(test_X)

# モデルの正解率
# 正解率は (モデルの予測した分類と実際の分類が一致したデータの数) ÷ (データの総数) で算出される
model.score(test_X, test_y)

機械学習用データの用意（ランダムデータで散布図）

2017年12月13日 by 河副太智 Leave a Comment

様々な分類の手法について実際にコードを動かして学ぶ際に、分類ができそうなデータを用意する必要があります。
実用レベルでは実際に測定された何かしらの値を入手するところから始めますが、今回はその部分は省き、架空の分類用データを自分で作成してしまいましょう。
分類に適したデータを作成するには、scikit-learn.datasetsモジュールのmake_classification() 関数を使います。

make_classificationの引数

# モジュールのimport
from sklearn.datasets import make_classification
# データX, ラベルyの生成
X, y = make_classification(n_samples, n_classes, n_features, n_redundant, random_state)
上記関数の各引数は以下のとおりです
n_samples
用意するデータの個数
n_classes
クラス数。デフォルトは2
n_features
データの特徴量の個数
n_redundant
分類に不要な特徴量（余分な特徴量）の個数
random_state
乱数のシード（乱数のパターンを決定する要素）
他にも引数はありますが、この章ではこれらを定義したデータを作成していきます。  
また、データがどのクラスに属しているかを示す「ラベル(y)」が用意されますが、基本的に整数値によってラベルを用意します。  
例えば二項分類であれば各データのラベルは「0」または「1」になります。

様々な分類の手法について実際にコードを動かして学ぶ際に、分類ができそうなデータを用意する必要があります。

実用レベルでは実際に測定された何かしらの値を入手するところから始めますが、今回はその部分は省き、架空の分類用データを自分で作成してしまいましょう。

分類に適したデータを作成するには、scikit-learn.datasetsモジュールのmake_classification() 関数を使います。

make_classificationの引数

# モジュールのimport

from sklearn.datasets import make_classification

# データX, ラベルyの生成

X, y = make_classification(n_samples, n_classes, n_features, n_redundant, random_state)

上記関数の各引数は以下のとおりです

n_samples

用意するデータの個数

n_classes

クラス数。デフォルトは2

n_features

データの特徴量の個数

n_redundant

分類に不要な特徴量（余分な特徴量）の個数

random_state

乱数のシード（乱数のパターンを決定する要素）

他にも引数はありますが、この章ではこれらを定義したデータを作成していきます。

また、データがどのクラスに属しているかを示す「ラベル(y)」が用意されますが、基本的に整数値によってラベルを用意します。

例えば二項分類であれば各データのラベルは「0」または「1」になります。

n_classes
クラス数。デフォルトは2
n_features
データの特徴量の個数
n_redundant
分類に不要な特徴量（余分な特徴量）の個数
random_state
乱数のシード（乱数のパターンを決定する要素）

# モジュールのimport
from sklearn.datasets import make_classification
# プロット用モジュール
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline

# コード
# データX, ラベルyを生成
X, y = make_classification(n_samples=50, n_features=2, n_redundant=0, random_state=0)

# データの色付け、プロット
plt.scatter(X[:, 0], X[:, 1], c=y, marker='.',
cmap=matplotlib.cm.get_cmap(name='bwr'), alpha=0.7)
plt.grid(True)

# モジュールのimport

from sklearn.datasets import make_classification

# プロット用モジュール

import matplotlib.pyplot as plt

import matplotlib

%matplotlib inline

# コード

# データX, ラベルyを生成

X, y = make_classification(n_samples=50, n_features=2, n_redundant=0, random_state=0)

# データの色付け、プロット

plt.scatter(X[:, 0], X[:, 1], c=y, marker='.',

cmap=matplotlib.cm.get_cmap(name='bwr'), alpha=0.7)

plt.grid(True)

他にも引数はありますが、この章ではこれらを定義したデータを作成していきます。  
また、データがどのクラスに属しているかを示す「ラベル(y)」が用意されますが、基本的に整数値によってラベルを用意します。  
例えば二項分類であれば各データのラベルは「0」または「1」になります。

他にも引数はありますが、この章ではこれらを定義したデータを作成していきます。

また、データがどのクラスに属しているかを示す「ラベル(y)」が用意されますが、基本的に整数値によってラベルを用意します。

例えば二項分類であれば各データのラベルは「0」または「1」になります。

DBSCAN

2017年12月12日 by 河副太智 Leave a Comment

k-means法は複雑で大小の偏りがある場合はよいクラスタリングができない事がある

これに対しクラスタリングのアルゴリズムにDBSCANがあり
クラスターを高密度(データが凝集している)の場所を低密度の場所から分離して表示

k-means法は、クラスターの大きさに均等で平坦な場合は有効だが
DBSCANは対照的に、平坦ではないデータやクラスターサイズに偏りがある際に真価を発揮する

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_moons
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN

# 月型のデータを生成
X, y = make_moons(n_samples=200, 
                 noise=0.05,
                 random_state=0)
# グラフと2つの軸を定義 左はk-means法用、右はDBSCAN用
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,3))
km = KMeans(n_clusters=2, random_state=0)
y_km = km.fit_predict(X)
ax1.scatter(X[y_km==0, 0],
            X[y_km==0, 1],
            c='lightblue',
            marker='o',
            s=40,
            label='cluster 1')
ax1.scatter(X[y_km==1, 0],
            X[y_km==1, 1],
            c='red',
            marker='s',
            s=40,
            label='cluster 2')
ax1.set_title('K-means clustering')

# DBSCAN用のインスタンスを生成


# XをDBSCANでクラスタリング


ax2.scatter(X[y_db==0, 0],
            X[y_db==0, 1],
            c='lightblue',
            marker='o',
            s=40,
            label='cluster 1')
ax2.scatter(X[y_db==1, 0],
            X[y_db==1, 1],
            c='red',
            marker='s',
            s=40,
            label='cluster 2')
ax2.set_title('DBSCAN clustering')
plt.legend()
plt.show()

import matplotlib.pyplot as plt

import numpy as np

from sklearn.datasets import make_moons

from sklearn.cluster import KMeans

from sklearn.cluster import DBSCAN

# 月型のデータを生成

X, y = make_moons(n_samples=200,

noise=0.05,

random_state=0)

# グラフと2つの軸を定義左はk-means法用、右はDBSCAN用

f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,3))

km = KMeans(n_clusters=2, random_state=0)

y_km = km.fit_predict(X)

ax1.scatter(X[y_km==0, 0],

X[y_km==0, 1],

c='lightblue',

marker='o',

s=40,

label='cluster 1')

ax1.scatter(X[y_km==1, 0],

X[y_km==1, 1],

c='red',

marker='s',

s=40,

label='cluster 2')

ax1.set_title('K-means clustering')

# DBSCAN用のインスタンスを生成

# XをDBSCANでクラスタリング

ax2.scatter(X[y_db==0, 0],

X[y_db==0, 1],

c='lightblue',

marker='o',

s=40,

label='cluster 1')

ax2.scatter(X[y_db==1, 0],

X[y_db==1, 1],

c='red',

marker='s',

s=40,

label='cluster 2')

ax2.set_title('DBSCAN clustering')

plt.legend()

plt.show()

SSEとエルボー法

2017年12月12日 by 河副太智 Leave a Comment

クラスタリングの性能評価関数にSSE(クラスタ内誤差平方和)がある
SSEにより様々なk-meansクラスタリングの性能を評価可能。

SSEの式
print(‘Distortion: %.2f’% km.inertia_)

クラスタ内誤差平方和を出力、クラスターの数を調整して一番低いものが正確

import matplotlib.pyplot as plt 
import numpy as np
import pandas as pd

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# Xには1つのプロットの(x,y)が、yにはそのプロットの所属するクラスター番号が入る
X,y = make_blobs(n_samples=150,         # サンプル点の総数
               n_features=2,          # 特徴量（次元数）の指定  default:2 
               centers=3,             # クラスタの個数
               cluster_std=0.5,       # クラスタ内の標準偏差 
               shuffle=True,          # サンプルをシャッフル
               random_state=0)        # 乱数生成器の状態を指定

km = KMeans(n_clusters=3,        # クラスターの個数
            init='k-means++',           # セントロイドの初期値をランダムに設定  default: 'k-means++'
            n_init=10,               # 異なるセントロイドの初期値を用いたk-meansの実行回数
            max_iter=300,            # k-meansアルゴリズムを繰り返す最大回数
            tol=1e-04,               # 収束と判定するための相対的な許容誤差
            random_state=0)          # 乱数発生初期化

y_km = km.fit_predict(X) # クラスターが存在するデータを渡し、各サンプルに対するクラスタ番号を求める

plt.scatter(X[y_km==0,0],         # y_km（クラスター番号）が0の時にXの0列目を抽出
                    X[y_km==0,1], # y_km（クラスター番号）が0の時にXの1列目を抽出
                    s=50,
                    c='r',
                    marker='*',
                    label='cluster 1')
plt.scatter(X[y_km==1,0],
                    X[y_km==1,1],
                    s=50,
                    c='b',
                    marker='*',
                    label='cluster 2')
plt.scatter(X[y_km==2,0],
                   X[y_km==2,1],
                    s=50,
                    c='g',
                    marker='*',
                    label='cluster 3')
plt.scatter(km.cluster_centers_[:,0],   # km.cluster_centers_には各クラスターのセントロイドの座標が入っている
                    km.cluster_centers_[:,1],
                    s=250,
                    marker='*',
                    c='black',
                    label='centroids')
plt.legend(loc="best")
plt.grid()
plt.show()

print('Distortion: %.2f'% km.inertia_) #クラスタ内誤差平方和を出力、クラスターの数を調整して一番低いものが正確

import matplotlib.pyplot as plt

import numpy as np

import pandas as pd

from sklearn.cluster import KMeans

from sklearn.datasets import make_blobs

# Xには1つのプロットの(x,y)が、yにはそのプロットの所属するクラスター番号が入る

X,y = make_blobs(n_samples=150, # サンプル点の総数

n_features=2, # 特徴量（次元数）の指定 default:2

centers=3, # クラスタの個数

cluster_std=0.5, # クラスタ内の標準偏差

shuffle=True, # サンプルをシャッフル

random_state=0) # 乱数生成器の状態を指定

km = KMeans(n_clusters=3, # クラスターの個数

init='k-means++', # セントロイドの初期値をランダムに設定 default: 'k-means++'

n_init=10, # 異なるセントロイドの初期値を用いたk-meansの実行回数

max_iter=300, # k-meansアルゴリズムを繰り返す最大回数

tol=1e-04, # 収束と判定するための相対的な許容誤差

random_state=0) # 乱数発生初期化

y_km = km.fit_predict(X) # クラスターが存在するデータを渡し、各サンプルに対するクラスタ番号を求める

plt.scatter(X[y_km==0,0], # y_km（クラスター番号）が0の時にXの0列目を抽出

X[y_km==0,1], # y_km（クラスター番号）が0の時にXの1列目を抽出

s=50,

c='r',

marker='*',

label='cluster 1')

plt.scatter(X[y_km==1,0],

X[y_km==1,1],

s=50,

c='b',

marker='*',

label='cluster 2')

plt.scatter(X[y_km==2,0],

X[y_km==2,1],

s=50,

c='g',

marker='*',

label='cluster 3')

plt.scatter(km.cluster_centers_[:,0], # km.cluster_centers_には各クラスターのセントロイドの座標が入っている

km.cluster_centers_[:,1],

s=250,

marker='*',

c='black',

label='centroids')

plt.legend(loc="best")

plt.grid()

plt.show()

print('Distortion: %.2f'% km.inertia_) #クラスタ内誤差平方和を出力、クラスターの数を調整して一番低いものが正確

しかし、この方法だと一度に一つのクラスタだけしか評価できないのでエルボー法により
forを10回回して10個分のSSEをグラフに表示させ、急降下している部分を見つける事が可能

import matplotlib.pyplot as plt 
import numpy as np
import pandas as pd

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# Xには1つのプロットの(x,y)が、yにはそのプロットの所属するクラスター番号が入る
X,y = make_blobs(n_samples=150,         # サンプル点の総数
               n_features=2,          # 特徴量（次元数）の指定  default:2 
               centers=3,             # クラスタの個数
               cluster_std=0.5,       # クラスタ内の標準偏差 
               shuffle=True,          # サンプルをシャッフル
               random_state=0)        # 乱数生成器の状態を指定

km = KMeans(n_clusters=3,        # クラスターの個数
            init='k-means++',           # セントロイドの初期値をランダムに設定  default: 'k-means++'
            n_init=10,               # 異なるセントロイドの初期値を用いたk-meansの実行回数
            max_iter=300,            # k-meansアルゴリズムを繰り返す最大回数
            tol=1e-04,               # 収束と判定するための相対的な許容誤差
            random_state=0)          # 乱数発生初期化

y_km = km.fit_predict(X) # クラスターが存在するデータを渡し、各サンプルに対するクラスタ番号を求める

distortions = []

for i  in range(1,11):                # 1~10クラスタまで一気に計算 
    km = KMeans(n_clusters=i,
                init='k-means++',     # k-means++法によりクラスタ中心を選択
                n_init=10,
                max_iter=300,
                random_state=0)
    km.fit(X)                         # クラスタリングの計算を実行
    distortions.append(km.inertia_)   # km.fitするとkm.inertia_が得られる

plt.plot(range(1,11),distortions,marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()

import matplotlib.pyplot as plt

import numpy as np

import pandas as pd

from sklearn.cluster import KMeans

from sklearn.datasets import make_blobs

# Xには1つのプロットの(x,y)が、yにはそのプロットの所属するクラスター番号が入る

X,y = make_blobs(n_samples=150, # サンプル点の総数

n_features=2, # 特徴量（次元数）の指定 default:2

centers=3, # クラスタの個数

cluster_std=0.5, # クラスタ内の標準偏差

shuffle=True, # サンプルをシャッフル

random_state=0) # 乱数生成器の状態を指定

km = KMeans(n_clusters=3, # クラスターの個数

init='k-means++', # セントロイドの初期値をランダムに設定 default: 'k-means++'

n_init=10, # 異なるセントロイドの初期値を用いたk-meansの実行回数

max_iter=300, # k-meansアルゴリズムを繰り返す最大回数

tol=1e-04, # 収束と判定するための相対的な許容誤差

random_state=0) # 乱数発生初期化

y_km = km.fit_predict(X) # クラスターが存在するデータを渡し、各サンプルに対するクラスタ番号を求める

distortions = []

for i in range(1,11): # 1~10クラスタまで一気に計算

km = KMeans(n_clusters=i,

init='k-means++', # k-means++法によりクラスタ中心を選択

n_init=10,

max_iter=300,

random_state=0)

km.fit(X) # クラスタリングの計算を実行

distortions.append(km.inertia_) # km.fitするとkm.inertia_が得られる

plt.plot(range(1,11),distortions,marker='o')

plt.xlabel('Number of clusters')

plt.ylabel('Distortion')

plt.show()

k-means

2017年12月12日 by 河副太智 Leave a Comment

k-means法でのクラスタリング

import matplotlib.pyplot as plt 
import numpy as np

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# Xには1つのプロットの(x,y)が、yにはそのプロットの所属するクラスター番号が入る
X,y = make_blobs(n_samples=150,         # サンプル点の総数
               n_features=2,          # 特徴量（次元数）の指定  default:2 
               centers=3,             # クラスタの個数
               cluster_std=0.5,       # クラスタ内の標準偏差 
               shuffle=True,          # サンプルをシャッフル
               random_state=0)        # 乱数生成器の状態を指定

km = KMeans(n_clusters=3, random_state=0)
y_km = km.fit_predict(X)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,3))

ax1.scatter(X[:, 0],
            X[:, 1],
            c='black')
ax1.grid()

ax2.scatter(X[y_km==0, 0],
            X[y_km==0, 1],
            c='r',
            s=40,
            label='cluster 1')
ax2.scatter(X[y_km==1, 0],
            X[y_km==1, 1],
            c='b',
            s=40,
            label='cluster 2')
ax2.scatter(X[y_km==2, 0],
            X[y_km==2, 1],
            c='g',
            s=40,
            label='cluster 3')
ax2.grid()
plt.show()

import matplotlib.pyplot as plt

import numpy as np

from sklearn.cluster import KMeans

from sklearn.datasets import make_blobs

# Xには1つのプロットの(x,y)が、yにはそのプロットの所属するクラスター番号が入る

X,y = make_blobs(n_samples=150, # サンプル点の総数

n_features=2, # 特徴量（次元数）の指定 default:2

centers=3, # クラスタの個数

cluster_std=0.5, # クラスタ内の標準偏差

shuffle=True, # サンプルをシャッフル

random_state=0) # 乱数生成器の状態を指定

km = KMeans(n_clusters=3, random_state=0)

y_km = km.fit_predict(X)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,3))

ax1.scatter(X[:, 0],

X[:, 1],

c='black')

ax1.grid()

ax2.scatter(X[y_km==0, 0],

X[y_km==0, 1],

c='r',

s=40,

label='cluster 1')

ax2.scatter(X[y_km==1, 0],

X[y_km==1, 1],

c='b',

s=40,

label='cluster 2')

ax2.scatter(X[y_km==2, 0],

X[y_km==2, 1],

c='g',

s=40,

label='cluster 3')

ax2.grid()

plt.show()