|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import cmath a = 12#aの数値 b = 23#bの数値 c = 25#cの数値 d = (b**2) - (4*a*c) sol1 = (-b-cmath.sqrt(d))/(2*a) sol2 = (-b+cmath.sqrt(d))/(2*a) print('結果 {0} と {1}'.format(sol1,sol2)) |
数学
平方根の計算
|
1 2 3 4 5 |
import cmath num = 9 #ここに数値を入れる num_sqrt = cmath.sqrt(num) print('{0} の平方根は {1:0.3f}+{2:0.3f}j'.format(num ,num_sqrt.real,num_sqrt.imag)) |
因数分解と素因数分解
因数分解
|
1 2 3 4 5 6 |
import sympy x = sympy.Symbol('x') eqn = x**2 - 3*x + 2 print(sympy.factor(eqn)) # (x - 2)*(x - 1) |
素因数分解
|
1 2 3 |
import sympy sympy.factorint(1000) #{2: 3, 5: 3} |
ユークリッド平面（原点0からの計算）
|
1 2 3 4 |
import numpy as np vec_a = np.array([2,0]) vec_b = np.array([0,2]) print(np.linalg.norm(vec_a + vec_b)) |
|
1 |
2.82842712475 |
コサイン類似度
コサイン類似度は、2つのベクトルがどれくらい似ているかの指標
2つのベクトル
a⃗ =(a1,a2,⋯,an)
b⃗ =(b1,b2,⋯,bn)
の場合以下の式になる
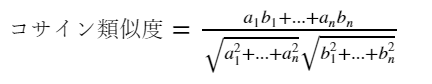
コサイン類似度を求める式
|
1 2 3 4 |
from scipy.spatial.distance import cosine vec_a = np.array([1, 2, 3]) vec_b = np.array([2, 3, 4]) print(1 - cosine(vec_a, vec_b)) |
ユークリッド距離を求める
|
1 2 3 4 5 6 7 8 9 10 |
>>> import numpy >>> x1 = 2 >>> y1 = 2 >>> x2 = 4 >>> y2 = 6 >>> a = numpy.array([x1, y1]) >>> b = numpy.array([x2, y2]) >>> u = b - a >>> numpy.linalg.norm(u) 4.4721359549995796 |
二点の座標がx(x1,x2),y(y1,y2)
のとき、これら二つの距離はピタゴラスの定理で求める
これをn次元空間における二点間にしたものがユークリッド距離
|
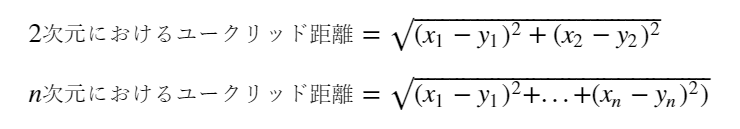
1 2 3 4 |
import numpy as np vec_a = np.array([1, 2, 3]) vec_b = np.array([2, 3, 4]) print(np.linalg.norm(vec_a - vec_b)) |
3次元で2点の座標が与えられた時2点間のユークリッド距離の求め方
- p(10,20,30),q(30,40,50)
|
1 2 3 4 |
import numpy as np vec_a = np.array([10, 20, 30]) vec_b = np.array([30, 40, 50]) print(np.linalg.norm(vec_a - vec_b)) |
上記コードは以下を計算する
|
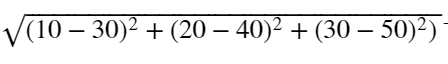
1 |