プログラミング

パラメーター multi_class　ロジステック回帰のハイパーパラメーター

2017年12月14日 by 河副太智 Leave a Comment

multi_classは多クラス分類を行う際にモデルがどういった動作を行うかということを決めるパラメーターです。
ロジスティック回帰では「ovr」、「multinomial」の2つの値が用意されています。
ovr
クラスに対して「属する/属さない」の二値で応えるような問題に適しています。
multinominal
各クラスに分類される確率も考慮され、「属する/属さない」だけではなく「どれくらい属する可能性があるか」を扱う問題に適しています。

パラメーター random_state　ロジステック回帰のハイパーパラメーター

2017年12月14日 by 河副太智 Leave a Comment

モデルは学習の際にデータをランダムな順番で処理していくのですが、random_stateはその順番を制御するためのパラメーターです。
ロジスティック回帰モデルの場合、データによっては処理順によって大きく境界線が変わる場合があります。

また、このrandom_stateの値を固定することで同じデータでの学習結果を保存することができます。
当講座でも実行時に結果が変わらないようにrandom_stateの値は基本的に固定しています。

当講座で用いているデータはrandom_stateを変えても結果があまり変わりませんが、実際に用いる場合にはデータの再現性も考えてrandom_stateの値を固定するとよいでしょう。

パラメーター penalty　ロジスティック回帰のハイパーパラメーター

2017年12月14日 by 河副太智 Leave a Comment

先ほどのCが分類の誤りの許容度だったのに対し、penaltyはモデルの複雑さに対するペナルティを表します。

penaltyに入力できる値は二つ、「l1」と「l2」です。
基本的には「l2」を選べば大丈夫ですが、「l1」を選ぶ方が欲しいデータが得られる場合もあります。
l1
データの特徴量を削減することで識別境界線の一般化を図るペナルティです。
l2
データ全体の重みを減少させることで識別境界線の一般化を図るペナルティです。

ペナルティとは、モデルが複雑になりすぎて一般化した問題を解決できなくなることを防ぐために与えられる。

パラメーター C　ロジスティック回帰のハイパーパラメーター

2017年12月14日 by 河副太智 Leave a Comment

ロジスティック回帰にはCというパラメーターが存在します。
このCはモデルが学習する識別境界線が教師データの分類間違いに対してどのくらい厳しくするのかという指標になります。

Cの値が大きいほどモデルは教師データを完全に分類できるような識別線を学習するようになります。
しかし教師データに対して過剰なほどの学習を行うために過学習に陥り、訓練データ以外のデータに予測を行うと正解率が下がる場合が多くなります。

Cの値を小さくすると教師データの分類の誤りに寛容になります。
分類間違いを許容することで外れ値データに境界線が左右されにくくなりより一般化された境界線を得やすくなります。
ただし、外れ値の少ないデータでは境界線がうまく識別できていないものになってしまう場合もあります。
また、極端に小さくてもうまく境界線が識別できません。

scikit-learnのロジスティック回帰モデルのCの初期値は1.0です。

import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
%matplotlib inline

# データの生成
X, y = make_classification(
    n_samples=1250, n_features=4, n_informative=2, n_redundant=2, random_state=42)
train_X, test_X, train_y, test_y = train_test_split(X, y, random_state=42)

# Cの値の範囲を設定(今回は1e-5,1e-4,1e-3,0.01,0.1,1,10,100,1000,10000)
C_list = [10 ** i for i in range(-5, 5)]

# グラフ描画用の空リストを用意
train_accuracy = []
test_accuracy = []

# 以下にコードを書いてください。
for C in C_list:
    model = LogisticRegression(C=C, random_state=42)
    model.fit(train_X, train_y)

    train_accuracy.append(model.score(train_X, train_y))
    test_accuracy.append(model.score(test_X, test_y))

# コードの編集はここまでです。
    
# グラフの準備
# semilogx()はxのスケールを10のx乗のスケールに変更する
plt.semilogx(C_list, train_accuracy, label="accuracy of train_data")
plt.semilogx(C_list, test_accuracy, label="accuracy of test_data")
plt.title("accuracy by changing C")
plt.xlabel("C")
plt.ylabel("accuracy")
plt.legend()
plt.show()

import matplotlib.pyplot as plt

from sklearn.linear_model import LogisticRegression

from sklearn.datasets import make_classification

from sklearn import preprocessing

from sklearn.model_selection import train_test_split

%matplotlib inline

# データの生成

X, y = make_classification(

n_samples=1250, n_features=4, n_informative=2, n_redundant=2, random_state=42)

train_X, test_X, train_y, test_y = train_test_split(X, y, random_state=42)

# Cの値の範囲を設定(今回は1e-5,1e-4,1e-3,0.01,0.1,1,10,100,1000,10000)

C_list = [10 ** i for i in range(-5, 5)]

# グラフ描画用の空リストを用意

train_accuracy = []

test_accuracy = []

# 以下にコードを書いてください。

for C in C_list:

model = LogisticRegression(C=C, random_state=42)

model.fit(train_X, train_y)

train_accuracy.append(model.score(train_X, train_y))

test_accuracy.append(model.score(test_X, test_y))

# コードの編集はここまでです。

# グラフの準備

# semilogx()はxのスケールを10のx乗のスケールに変更する

plt.semilogx(C_list, train_accuracy, label="accuracy of train_data")

plt.semilogx(C_list, test_accuracy, label="accuracy of test_data")

plt.title("accuracy by changing C")

plt.xlabel("C")

plt.ylabel("accuracy")

plt.legend()

plt.show()

k-nn構築

2017年12月13日 by 河副太智 Leave a Comment

k-NNはk近傍法とも呼ばれ、予測をするデータと類似したデータをいくつか見つけ、多数決により分類結果を決める手法です。
怠惰学習と呼ばれる学習の種類の一手法であり、学習コスト（学習にかかる計算量）が0であることが特徴です。

これまで紹介してきた手法とは違い、k-NNは教師データから学習するわけではなく、予測時に教師データを直接参照してラベルを予測します。
結果の予測を行う際に①教師データを予測に用いるデータとの類似度で並べ直し、②分類器に設定されたk個分のデータを類似度の高い順に参照し、③参照された教師データが属するクラスのなかで最も多かったものを予測結果として出力する
のがこのk-NNという手法です。

k-NNの特徴としては、前述の通り学習コストが0であること、アルゴリズムとしては比較的単純なものなのですが高い予測精度がでやすいこと、複雑な形の境界線も表現しやすいことが挙げられます。
欠点としては分類器に指定する自然数kの個数を増やしすぎると識別範囲の平均化が進み予測精度が下がってしまう点や、予測時に毎回計算を行うため教師データや予測データの量が増えると計算量が増えてしまい、低速なアルゴリズムとなってしまう点が挙げられます。

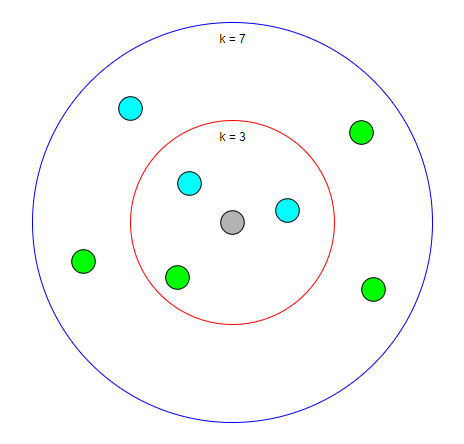
以下の画像は、kの数の違いによる分類過程の様子の違いを表しています。
灰色の点はk=3の時では水色の点の方が周りに多いため水色の点だと予測されますが、k=7の時では緑色の点の方が多いため緑色の点ではないかという予測に変わります。

# きのこデータの取得
import requests
import zipfile
from io import StringIO
import io
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn import preprocessing

# url
mush_data_url = "http://archive.ics.uci.edu/ml/machine-learning-databases/mushroom/agaricus-lepiota.data"
s = requests.get(mush_data_url).content

# データの形式変換
mush_data = pd.read_csv(io.StringIO(s.decode('utf-8')), header=None)

# データに名前をつける(データを扱いやすくするため)
mush_data.columns = ["classes", "cap_shape", "cap_surface", "cap_color", "odor", "bruises",
"gill_attachment", "gill_spacing", "gill_size", "gill_color", "stalk_shape",
"stalk_root", "stalk_surface_above_ring", "stalk_surface_below_ring",
"stalk_color_above_ring", "stalk_color_below_ring", "veil_type", "veil_color",
"ring_number", "ring_type", "spore_print_color", "population", "habitat"]

# 参考（カテゴリー変数をダミー特徴量として変換する方法）
mush_data_dummy = pd.get_dummies(
mush_data[['gill_color', 'gill_attachment', 'odor', 'cap_color']])
# 目的変数：flg立てをする
mush_data_dummy["flg"] = mush_data["classes"].map(
lambda x: 1 if x == 'p' else 0)

# 説明変数と目的変数
X = mush_data_dummy.drop("flg", axis=1)
Y = mush_data_dummy['flg']

# 学習データとテストデータに分ける
train_X, test_X, train_y, test_y = train_test_split(X,Y, random_state=42)

# モデルの読み込み
from sklearn.neighbors import KNeighborsClassifier

# モデルの構築
model = KNeighborsClassifier()
# モデルの学習
model.fit(train_X, train_y)

# 正解率の表示
print(model.score(test_X, test_y))

# きのこデータの取得

import requests

import zipfile

from io import StringIO

import io

import pandas as pd

from sklearn.model_selection import train_test_split

from sklearn import preprocessing

# url

mush_data_url = "http://archive.ics.uci.edu/ml/machine-learning-databases/mushroom/agaricus-lepiota.data"

s = requests.get(mush_data_url).content

# データの形式変換

mush_data = pd.read_csv(io.StringIO(s.decode('utf-8')), header=None)

# データに名前をつける(データを扱いやすくするため)

mush_data.columns = ["classes", "cap_shape", "cap_surface", "cap_color", "odor", "bruises",

"gill_attachment", "gill_spacing", "gill_size", "gill_color", "stalk_shape",

"stalk_root", "stalk_surface_above_ring", "stalk_surface_below_ring",

"stalk_color_above_ring", "stalk_color_below_ring", "veil_type", "veil_color",

"ring_number", "ring_type", "spore_print_color", "population", "habitat"]

# 参考（カテゴリー変数をダミー特徴量として変換する方法）

mush_data_dummy = pd.get_dummies(

mush_data[['gill_color', 'gill_attachment', 'odor', 'cap_color']])

# 目的変数：flg立てをする

mush_data_dummy["flg"] = mush_data["classes"].map(

lambda x: 1 if x == 'p' else 0)

# 説明変数と目的変数

X = mush_data_dummy.drop("flg", axis=1)

Y = mush_data_dummy['flg']

# 学習データとテストデータに分ける

train_X, test_X, train_y, test_y = train_test_split(X,Y, random_state=42)

# モデルの読み込み

from sklearn.neighbors import KNeighborsClassifier

# モデルの構築

model = KNeighborsClassifier()

# モデルの学習

model.fit(train_X, train_y)

# 正解率の表示

print(model.score(test_X, test_y))

機械学習　教師ありの基本的な記述

2017年12月13日 by 河副太智 Leave a Comment

教師ありの機会学習の際の基本的な構造は以下のようになる

# 学習データとテストデータに分ける
train_X, test_X, train_y, test_y = train_test_split(X,Y, random_state=42)

# モデルの読み込み
from sklearn.neighbors import KNeighborsClassifier

# モデルの構築
model = KNeighborsClassifier()#学習内容によって変わる
# モデルの学習
model.fit(train_X, train_y)#学習データがはいる

# 正解率の表示
print(model.score(test_X, test_y))#テストデータが入る

# 学習データとテストデータに分ける

train_X, test_X, train_y, test_y = train_test_split(X,Y, random_state=42)

# モデルの読み込み

from sklearn.neighbors import KNeighborsClassifier

# モデルの構築

model = KNeighborsClassifier()#学習内容によって変わる

# モデルの学習

model.fit(train_X, train_y)#学習データがはいる

# 正解率の表示

print(model.score(test_X, test_y))#テストデータが入る