a
|
1 |
math.log(math.sqrt(27),3) |
b
|
1 |
math.log(3/4,3)+4*math.log(3/math.sqrt(2)) |
数学
累乗と累乗根
\(4^{4}\times 2^{-1}\div 2^{2}\)
|
1 2 3 4 |
# 4**4*2**-1/2**2 Out:32 |
\(\sqrt [4] {81}\)
|
1 2 3 4 |
# pow(81, 1/4) OUT:3 |
\(\sqrt [3] {81}\times \sqrt [3] {9}\)
|
1 2 3 4 |
# pow(81,1/3)*pow(9,1/3) out:8.99999999 |
\(\sqrt [3] {\sqrt {64}}\)
|
1 2 3 4 |
# pow(pow(64,1/2),1/3) out:2 |
展開
を展開する場合は
|
1 |
sympy.expand(2*b*(x + 2)*(x - 4)) |
Out:
|
1 |
2*b*x**2 - 4*b*x - 16*b |
因数分解
因数分解一問目
|
1 2 3 4 5 |
import sympy x,y,z,a,b = sympy.symbols('x,y,z,a,b') A4 = 2*b*x**2-4*b*x-16*b sympy.factor(A4) |
OUT:
|
1 |
2*b*(x - 4)*(x + 2) |
因数分解二問目
|
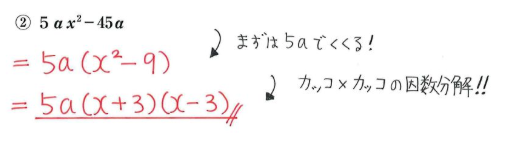
1 2 |
A5 = 5*a*x**2-45*a sympy.factor(A5) |
OUT:
|
1 |
5*a*(x - 3)*(x + 3) |
素数判定プログラム
フェルマーの小定理での素数判定は５行でできる
|
1 2 3 4 5 6 |
val = 6 if pow(2, val-1)% val == 1: print("{0}: 素数".format(val)) else: print("{0}: 素数ではない".format(val)) |
普通に判定すると以下のようになる
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
val= 6 cnt = 0 for a in range(2, val+1): cnt += 1 if a*a > val: # (1) result= True break if val% a == 0: result = False break if result: print ("{0}: 素数：({1})".format(val, cnt)) else: print("{0}: 素数ではない：({1})".format(val, cnt)) |
素因数分解
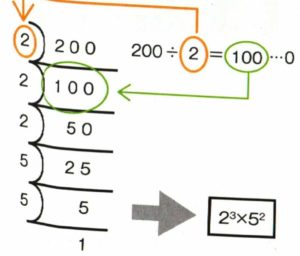
200を素因数分解すると
2^3 x 5^2が答えである
これをpythonで書くと以下のようになる
|
1 2 |
import sympy as sym sym.factorint(200) |
|
1 |
{2: 3, 5: 2} |
